概述
先给「不开窍」下个定义:
努力学习,难以理解。
这样的同学,在数学上付出了大量时间和精力,有学习的意愿和行动。然而,就是很难理解数学,只能靠死记硬背反复刷题。
本训练营旨在回归数学的本质,让同学们可以理解概念、搞懂错题、攻克难题、发展智慧、越学越聪明。
不仅仅实现数学学习优秀,而且在跨学科的自主学习研究思考能力上精进。
知识体系内化法
今天同学的数学学习困境,根源在于知识内化能力不足,反复刷题并没有解决知识消化能力弱的问题,反而因为增大的任务量,导致更难有时间研究理解消化知识,形成恶性循环。
为解决此问题,我研发了「5页纸的知识体系内化法」,作为高质量学习的核心评估标准和实践指南。
其要诀如下:
- 目标:海纳百川,炼成融汇贯通知识体系
- 战略:3个通透(知识通透、脉络通透、题目通透)
- 战术:3步实操(寻宝、连线、占领)
- 寻宝:吃透3种知识(来源、本体、应用)
- 连线:吃透两大脉络(演化脉络、结构脉络)
- 占领:吃透3种题目(基础题、难题、错题)
训练营的核心目标,就是训练同学深度理解和掌握这套方法,能够持续应用到学习中,升级自己的学习研究能力,并在此基础上形成融汇贯通的知识体系。
它既是训练营的起点,也是训练营的终点。请务必首先阅读这5页纸全文,从而清晰的了解自身或者孩子当前学习的低效根源,明确发展的方向。
全文阅读:5页纸数学开窍
知识森林学习系统
知识体系内化法,是基于顶尖学习者的学习方式来做反向分析提炼的。
这套方法,对于顶尖的同学而言,他们头脑抽象能力强,往往在头脑中就可以高效实现这3步研究流程,因此也大多数人觉得是「神级表现」。
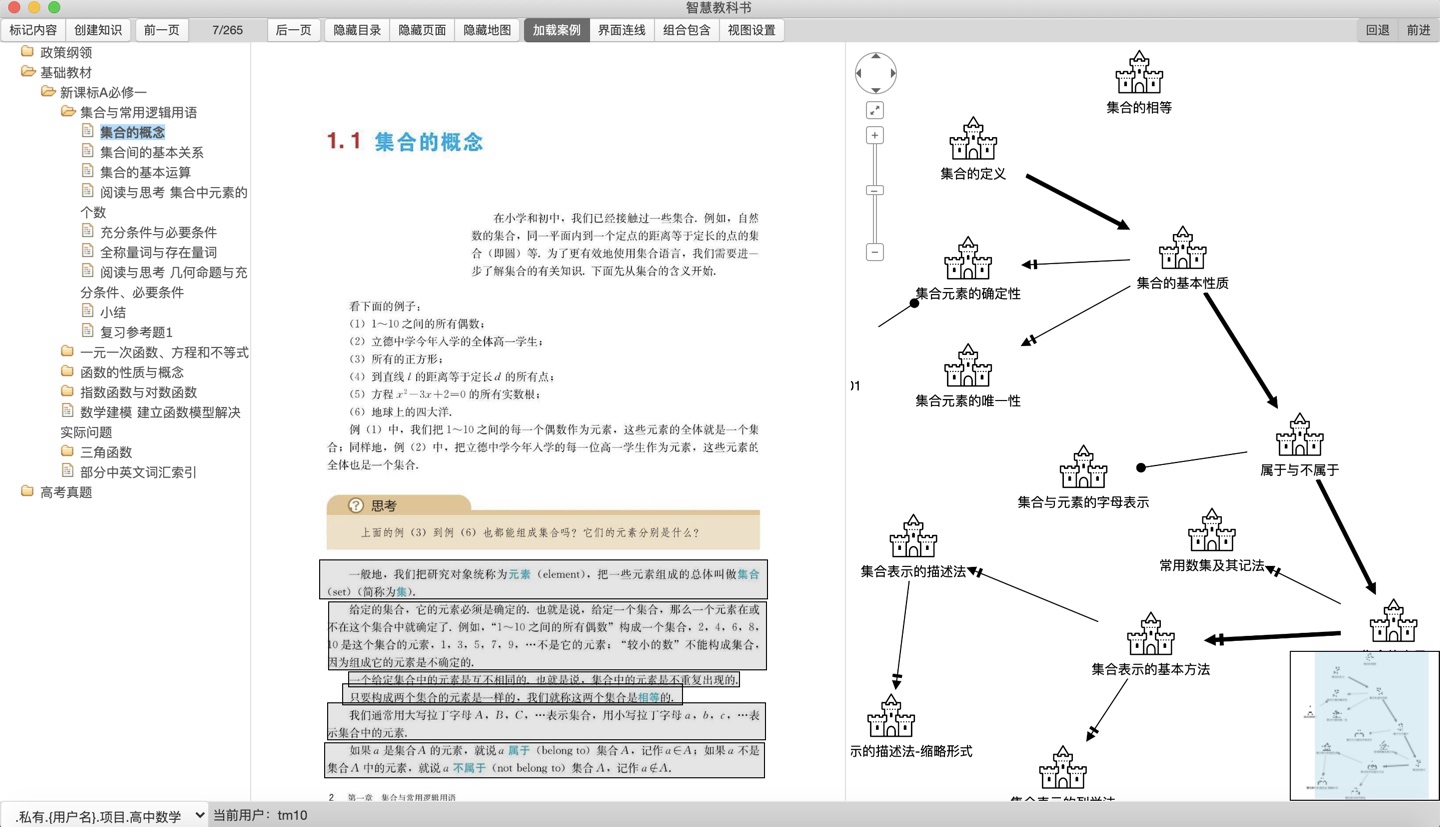
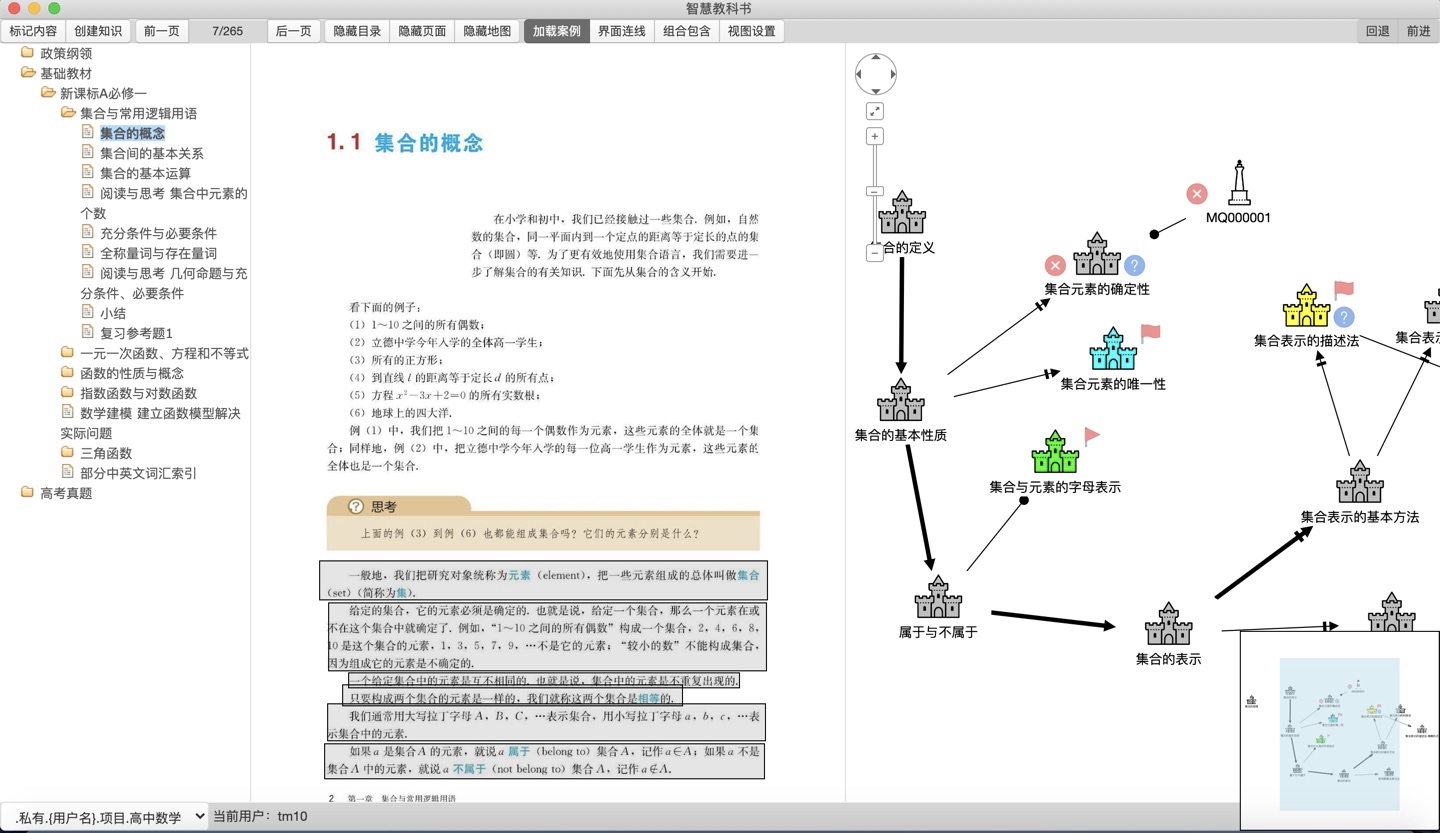
然而对于更多的同学,要实现这样以知识体系建构为核心的研究学习,一个核心难点是「知识体系看不见摸不着」,因此「吃透知识和吃透脉络」变得很困难。相对而言「吃透题目」的学习反而更容易,因为单独解题的训练,可以比较零散的进行。而知识体系的整体研究分析,却需要更系统更直观。
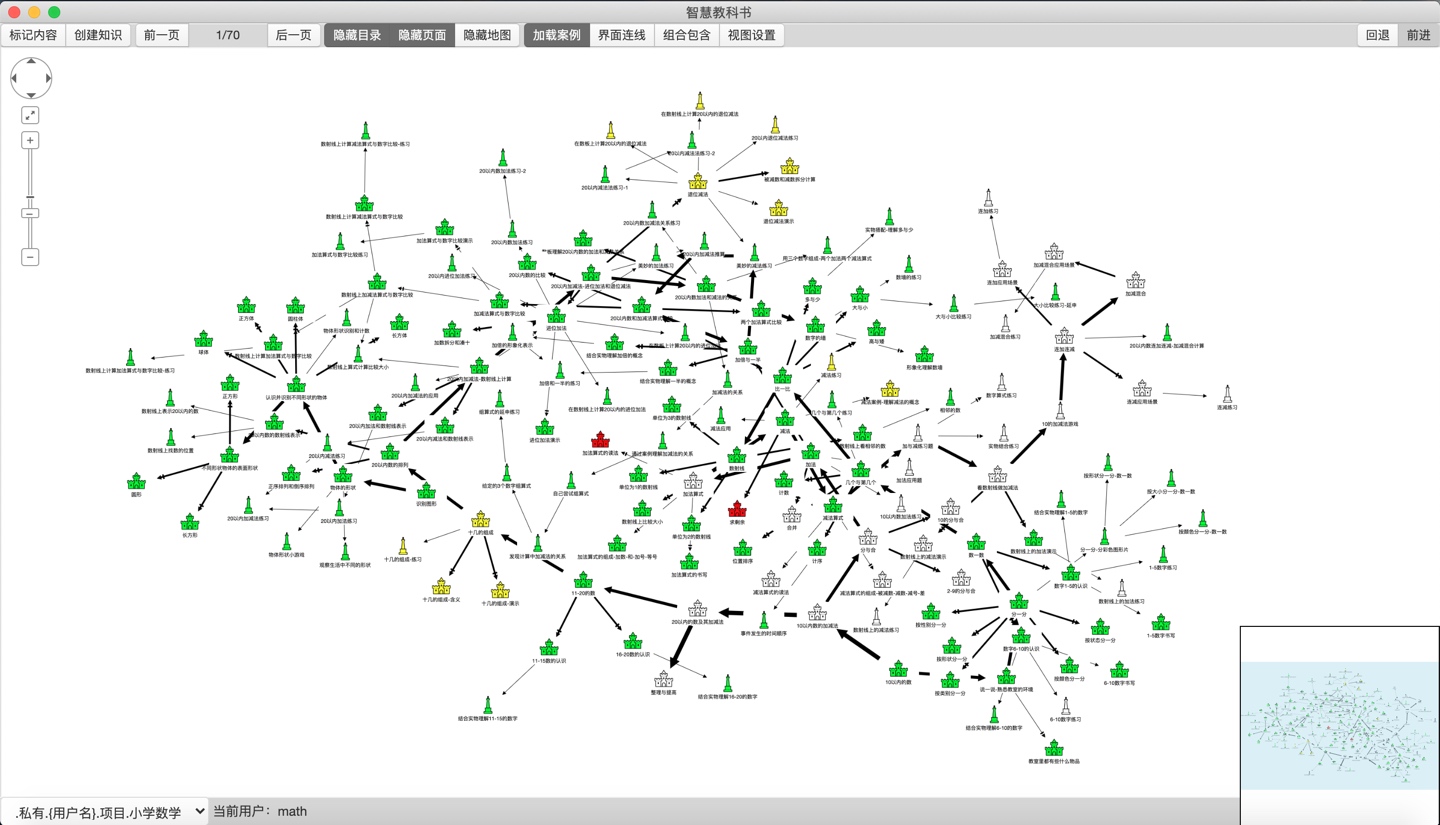
为此我研发了知识森林学习软件,根除了这一问题。
具体来说,它实现了知识体系建设的四化。
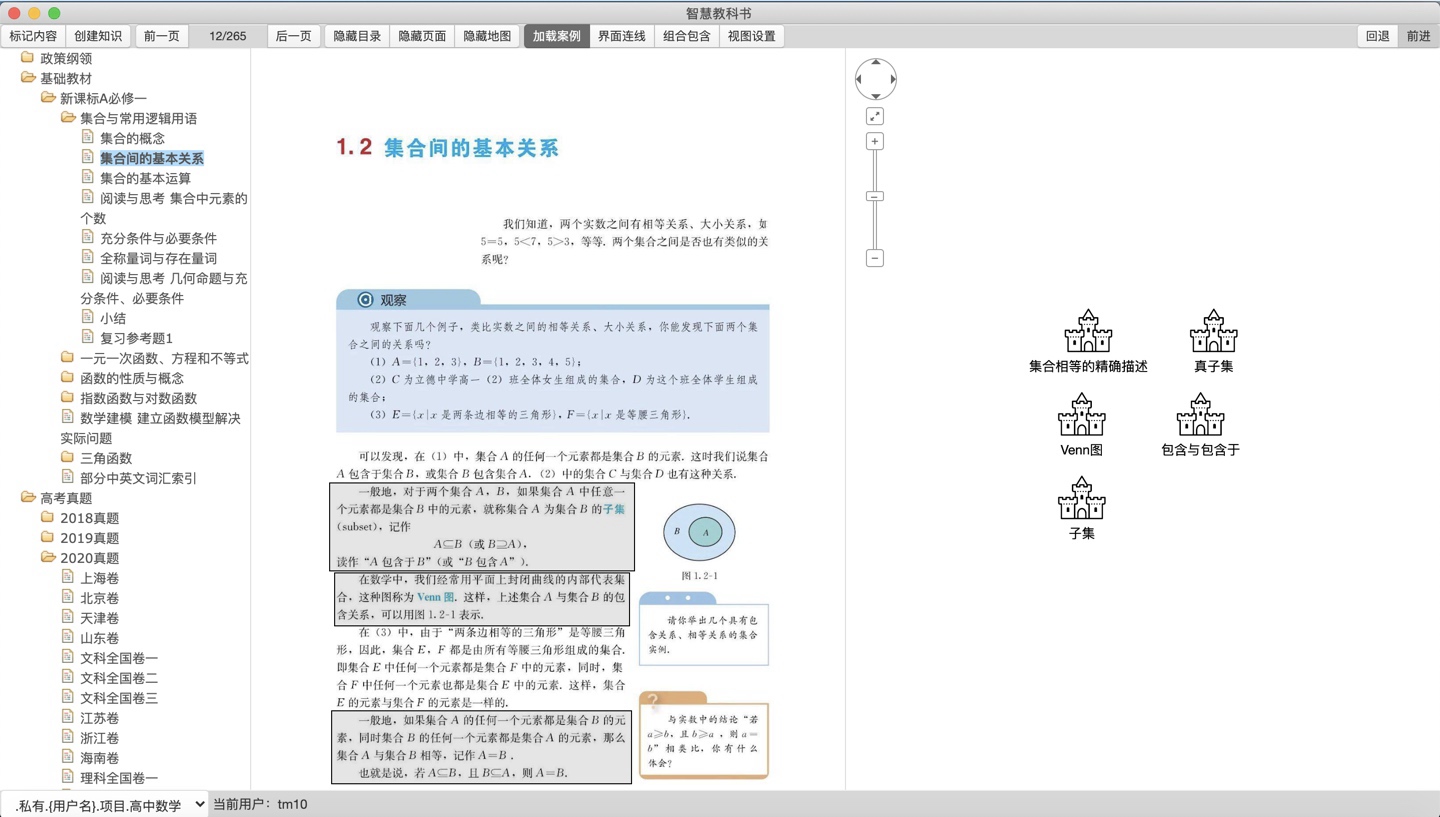
1)知识体系可视化
2)知识建构集成化
3)题目分析集成化
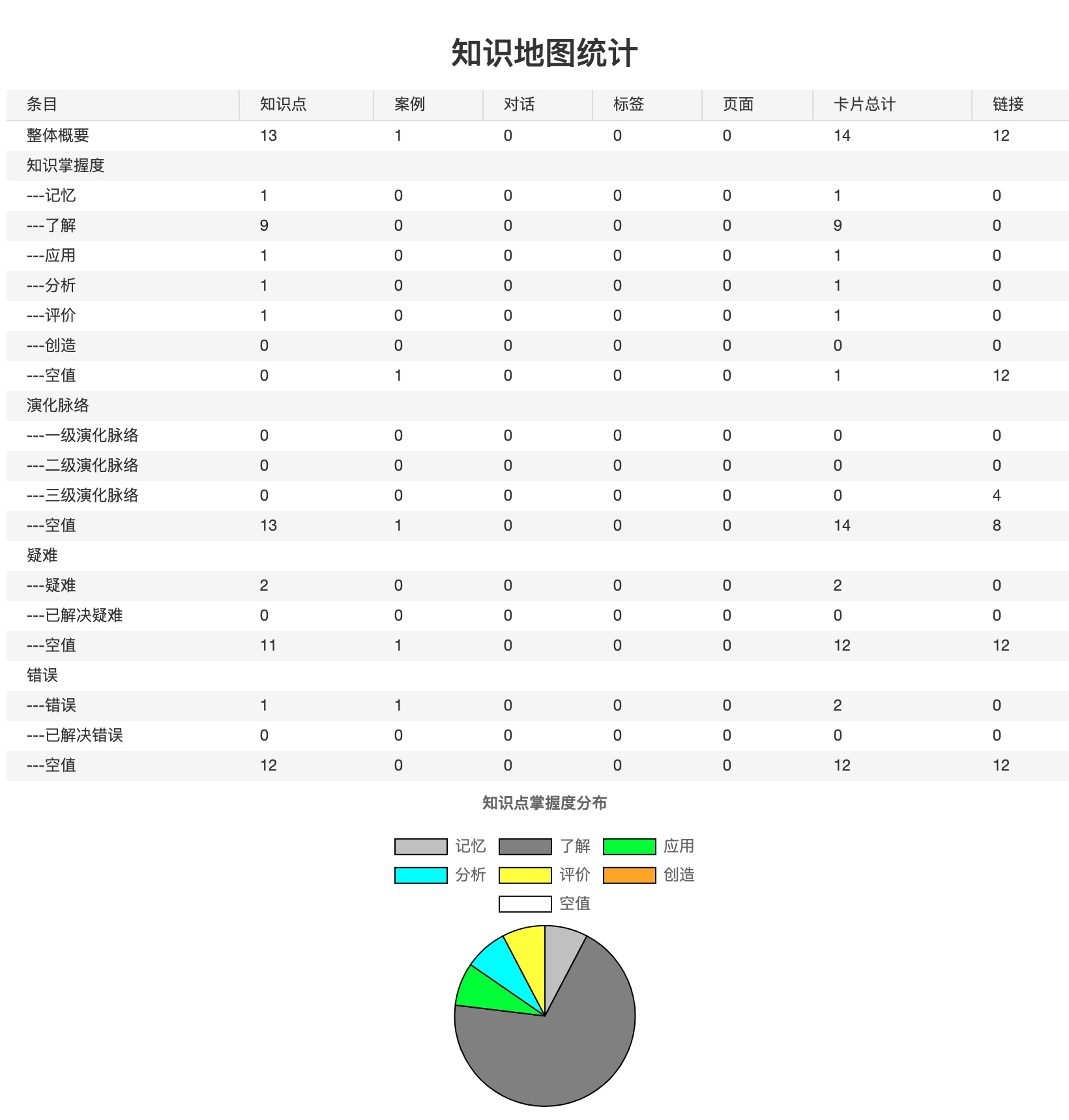
4)数据统计精准化
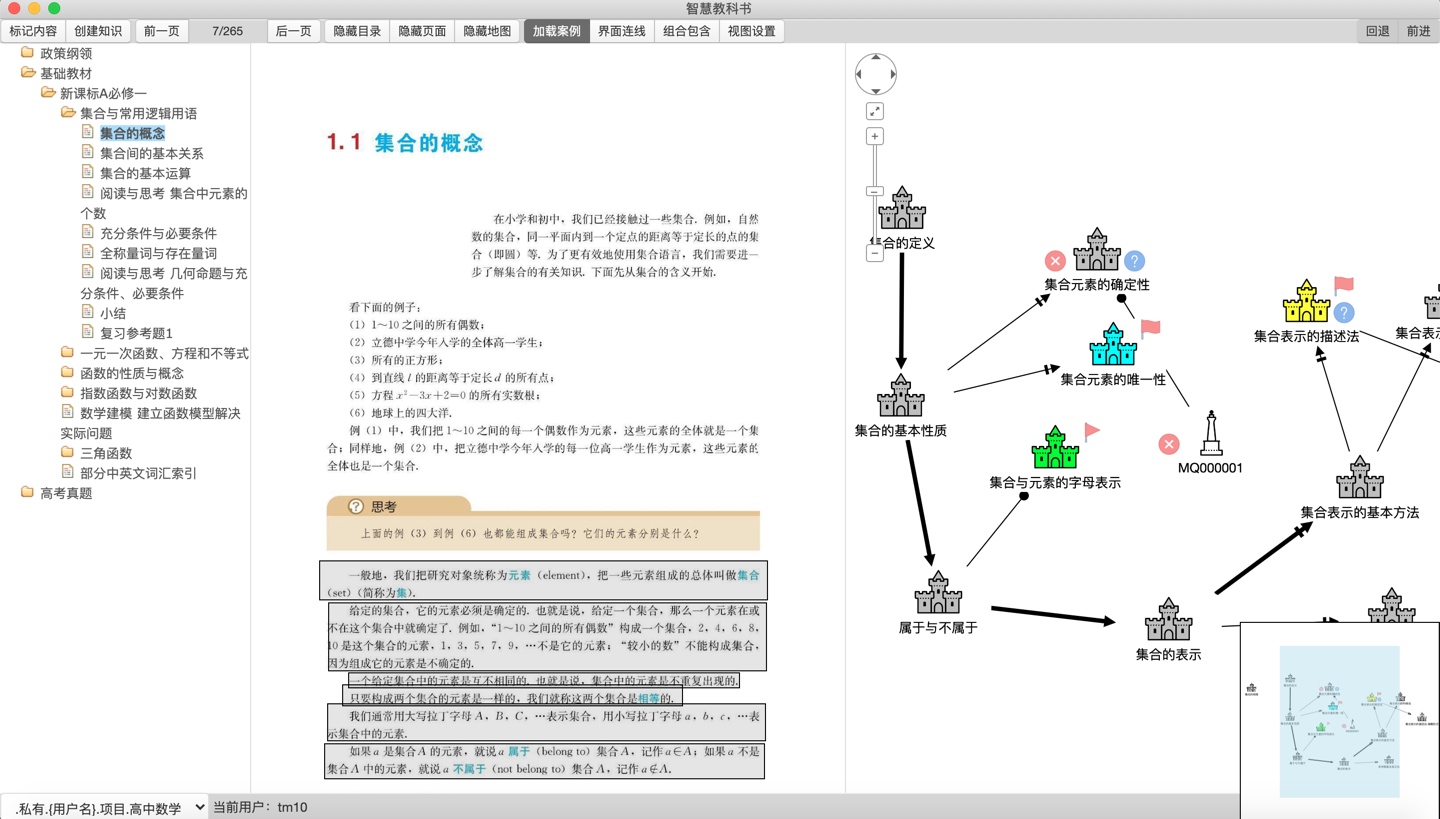
同时,在知识森林学习系统中,继承了AI学习伙伴功能。
有了AI加持,同学们可以在研究知识点、分析知识脉络时得到24×7的支持,生产力进一步升级,再次实现对传统学习方式的降维打击。
知识森林学习软件就像是工业革命时代的铁甲船,AI就像是蒸汽机。当年蒸汽机+铁甲船的组合,让英国把商船和炮舰开到了全世界,对木制帆船实现了碾压。
在这个背景下,首要的事情,就是点开科技树,开启你学习上的大航海时代。
关于寻宝连线占领学习方法论和知识森林学习系统更进一步的介绍,可以阅读文章不刷题不补习数学开窍
视频课程安排
本训练营围绕4个开窍组织,分为6个模块。
| 时段 |
主题 |
愚昧 |
开窍 |
| 第一部分 |
规则的开窍 |
蛮力游戏 |
智力游戏 |
| 第二部分 |
知识的开窍(上) |
死记硬背 |
整体理解 |
| 第三部分 |
知识的开窍(中) |
死记硬背 |
整体理解 |
| 第四部分 |
知识的开窍(下) |
死记硬背 |
整体理解 |
| 第五部分 |
难题的开窍 |
复制答案 |
有效简化 |
| 第六部分 |
错题的开窍 |
订正答案 |
溯本求源 |
知识的开窍拆分为了3个部分,因为这部分是最基础也是最重要的,而又却是被应试教育完全忽视的,因此必须作为重中之重学习研究实践。
整体视频课时长规划为25小时,视频课中附带一系列随堂作业,请以50小时作为随堂作业量的大致估计。
随堂作业的很多内容,都是围绕「自主建构知识体系」这一大作业,要做的阶段性工作,例如为了实践「寻宝连线方法论」,在课程中以初中数学第一章「有理数」作为基本案例,因此「有理数」一章的知识体系深度建构,也就放在了随堂作业中。
这样的阶段性知识建构作业,也为后续同学在日常学习中持续提炼知识形成体系打下基础。
整体计算,课程基本学习时间(视频课+随堂作业)以75小时作为粗略估计。
课程大纲
第一部分:规则的开窍
- 视频:追求高分还是追求聪明
- 视频:自由的人与爱智的心
- 视频:3个层次的爱智求真
- 视频:泰斯勒求真要从经验到概念
- 视频:泰斯勒求真要善于建模
- 视频:泰斯勒求真要对观点做证明
- 视频:毕达哥拉斯求真要数形结合
- 视频:希帕索斯求真要反向思考
- 视频:苏格拉底求真要了解自己的无知
- 视频:苏格拉底求真要深入的调研
- 视频:柏拉图求真要追求永恒
- 视频:亚里士多德求真要建立跨学科体系
- 视频:亚里士多德求真要逻辑清晰
- 视频:亚里士多德求真要溯本思考
- 视频:托勒密求真要创造研究环境
- 视频:欧几里得求真要推导知识森林
- 视频:求真智力发展的学习模型
第二部分:知识的开窍(上)
- 视频:搬运知识还是种植知识
- 视频:知识脉络推导之数的概念的产生
- 视频:知识脉络推导之十进制的产生
- 视频:知识脉络推导之加法的产生
- 视频:知识脉络推导之减法的产生
- 视频:知识脉络推导之乘法的产生
- 视频:知识脉络推导之除法的产生
- 视频:知识脉络推导之四则运算的产生
- 作业:总结知识体系推导实践要点
- 作业:推导算术核心知识脉络
第三部分:知识的开窍(中)
- 视频:3张地图打通知识体系
- 视频:知识森林网页版快速上手
- 作业:创建知识演化脉络地图
第四部分:知识的开窍(下)
- 作业:创建数学教材知识建构项目
- 作业:创建学习资料目录树
- 作业:创建学习资料
- 视频:寻宝操作入门
- 视频:全面寻宝
- 作业:对正数和负数一节全面寻宝
- 视频:WWH深入理解知识
- 视频:AI辅助识别知识
- 视频:知识森林概念入门
- 视频:连线操作入门
- 视频:正数与负数一节演化脉络推导
- 作业:正数与负数一节演化脉络推导
- 视频:AI辅助研究提炼演化脉络
- 视频:7要素模型辅助提炼知识脉络
- 视频:正数与负数一节提炼结构脉络
- 作业:正数与负数一节提炼结构脉络
- 视频:AI辅助研究提炼结构脉络
- 视频:知识体系审视与优化
- 作业:正数与负数一节知识体系审视与优化
- 视频:WWH学透基础题
- 作业:正数与负数一节学透3道基础题
- 作业:提炼建构有理数一章知识体系
第五部分:难题的开窍
- 视频:WWH学透难题
- 作业:运用WWH学透难题
- 日常案例学习:经典难题分析研究
第六部分:错题的开窍
- 视频:WWH学透错题
- 作业:运用WWH学透错题
- 日常案例学习:经典错题分析研究
说明:此大纲为草案版,根据教学需要具体细节可能会有调整。
实践大作业:建构数学学科知识体系
「知识体系内化法」的核心目标,是「海纳百川,炼成融汇贯通知识体系」,这不仅仅是课程训练的目标,也应该是同学们学习数学课程的核心实践目标。
因此课程的设计,其实就是围绕「建成通透知识体系」这一大目标来的。
课程的视频内容围绕此目标组织,来传授学习思想和方法,工具的应用。课程中的随堂作业,也为此而布置。
但是课程本身,直接布置的随堂作业是有限的,不可能覆盖所有的数学章节。而是重点在于分享经典案例,教授同学方法,初步实践掌握之后,可以迁移到日常的数学学习中,持续提炼建构知识体系,并且进一步的通过实践提高对学习思想和方法的掌握程度。
因此这一实践大作业,跨越了训练营教学和同学日常课堂学习,这也是我们学以致用,用以促学的融汇贯通。
教学方式与授课安排
- 授课:在线视频课(录播)
- 工具:知识森林学习系统
- 大作业:建构数学学科知识体系
- 讨论:微信群
目前第一部分到第四部分核心授课内容已经录制完成,剩余计划在7月底之前录制完成。
整体计划:视频课25小时,随堂作业50小时。
课程在线学习系统
视频课程放在在线学习系统中,报名后会开设账号。
家长和同学可以自行安排时间学习。

设备要求
1)视频课的设备需求
手机、平板和电脑都可以访问学习。
2)知识森林学习系统的设备需求
部分作业涉及到使用知识森林学习系统,研究提炼建构知识体系。
知识森林学习软件支持大多数平板和电脑,但不支持手机(因为知识建构界面知识地图本身就需要比较大的空间,手机不足以显示)。
为了更好的效果,建议使用13寸及以上的平板或者电脑,或者外接13寸及以上的显示器。
在知识森林学习软件中,对于拖拉创建知识点之类的操作,需要触控板或者鼠标,最好配置键盘以便打字方便。
产品与价格
训练营包含课程以及学习系统。定价如下:
- 8,800元(包含半年的知识森林学习系统AI版使用权)
- 12,800元(包含一年的知识森林学习系统AI版使用权)
知识森林学习系统是围绕「寻宝连线占领」的精准学习方法论,自主研发的以知识体系建设为核心的学习软件,全球顶尖的理科学习系统,内置AI学习研究助手,和AI一起高速学习研究进化。
如果按时保质完成学习,半年到一年时间已经足以实现自主学习、研究和思考的能力升级。
后续如需继续使用知识森林AI版,费用为12,800元/年。
老师介绍
徐强,知识森林学习软件创始人,知乎30万关注者,前微软工程师。
致力于创造出高度赋能于人,实现心智发展的创新教育。研发「知识体系内化法」理论,致力于实现发展心智水平,打通知识体系的新学习方法。
著有电子书《高中生,3步打通理科思维》。该书在知乎书店、微信读书等平台已上线。
研发知识森林学习软件,整合AI科技,以形象化数字化的方式来实现知识体系建构学习,落实知识体系内化法。
不同学龄学习建议
小学1-3年级,推荐家长自己学习,在孩子日常学习的辅导中引导孩子,部分形成自主学习能力。基于家长的进步带动孩子的进步。不追求孩子能自主提炼形成知识体系,而是在家长引导下学习推导知识,形成推导分析意识。
小学4-6年级,推荐家长和孩子一起学习研讨,家长在辅导中引导孩子,逐渐形成自主学习意识和能力。
初高中,推荐孩子自主学习。但如果本身家长在参与孩子的学习辅导,那么可以一起学习讨论,过渡到孩子自主学习研究。
这种过渡应该在三个月到一年内完成。实现家长和老师对孩子「扶上马,送一程」,赋能他们自主学习研究,这样孩子学习能力上去,自学责任到位,大家都轻松省力高效。
无论在什么学龄,家长应该基于「5页纸知识体系内化法」的标准,参与到对孩子学习质量的关注和支持中。
课程咨询与报名
关于课程的核心理念,请首先阅读文章5页纸数学开窍。
关于「知识体系内化法」和「知识森林学习软件」进一步的介绍,请阅读文章不刷题不补习数学开窍。
咨询或报名请添加微信johnxuqiang,或者直接扫码添加,添加时请备注「数学开窍」。